信号模型

BS-UE 信道建模为：

$$ {h}_{\mathrm{UE}}\left( t,\tau \right) =\sum_{l=1}^L{\alpha _l\delta \left( \tau -\tau _l-\tau _d \right) e^{j2\pi \left( f_{D,l}+\Delta f_c \right) t}} $$

其中 \(L\) 是多径分量的数量，\(\tau_d\) 是定时偏差，\(\Delta f_c\) 是载波频率偏差。

单站感知信道为：

$$ {h}_{\mathrm{BS}}\left( t,\tau \right) =\sum_{p=1}^P{\beta _{p}\delta \left( \tau -\tau _{s,p} \right) e^{j2\pi f_{D,s,p} t}} $$

连续波与分组无线电

OpenISAC 采用连续波传输方案，以实现更精确和灵活的多普勒感知，避免了基于分组的系统（如 Wi-Fi）的抖动和不规则间隔。

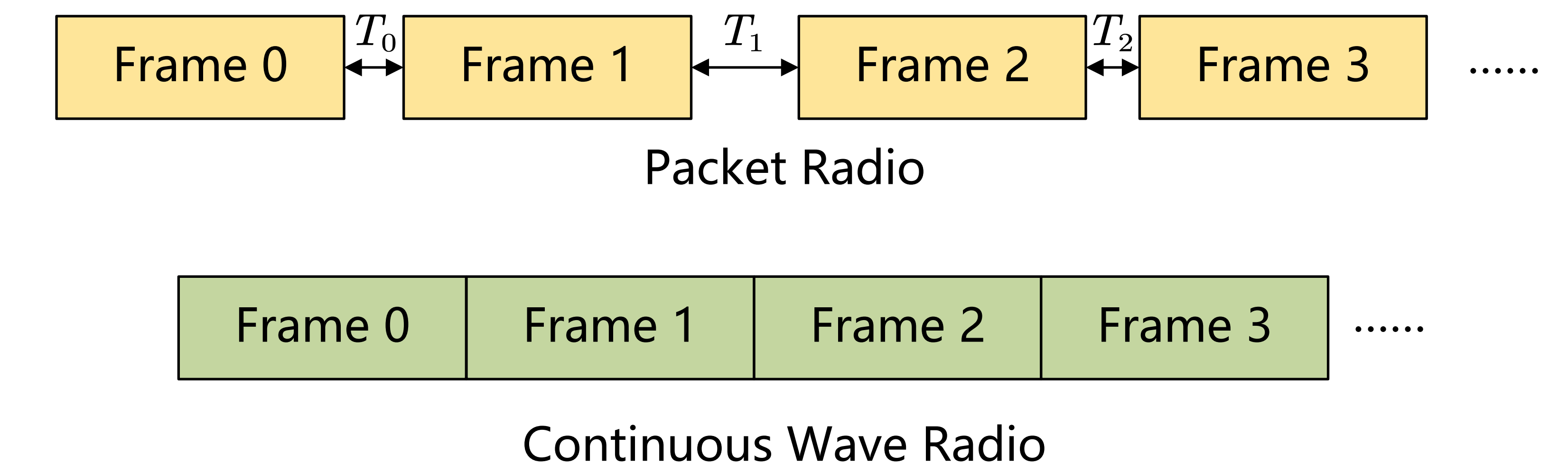
Packet Radio vs Continuous Wave

图 4. 分组无线电与连续波无线电的比较。

单站感知

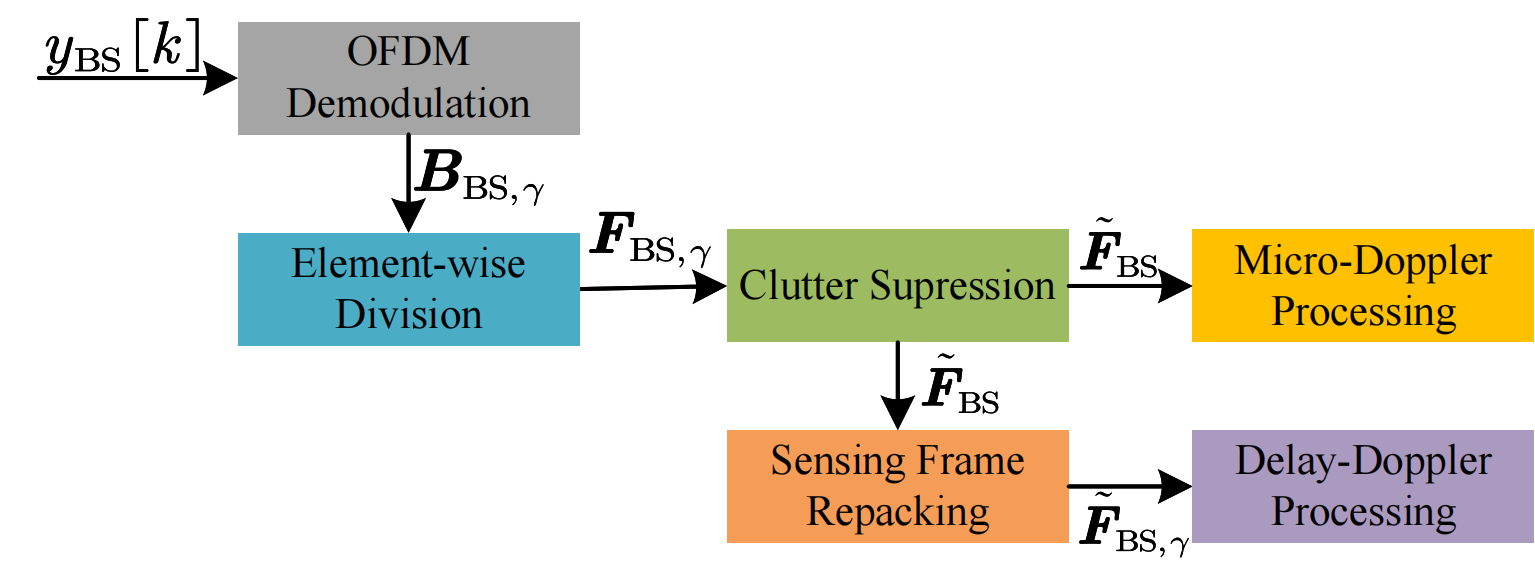
Monostatic Sensing Flow Graph

图 5. 单站感知的信号处理流程。

处理流程包括：

  1. OFDM 解调与逐元素除法： 消除发送数据符号的影响以获得时频信道矩阵。 $$ \left( \boldsymbol{F}_{\mathrm{BS},\gamma} \right) _{n,m}=\frac{\left( \boldsymbol{B}_{\mathrm{BS},\gamma} \right) _{n,m}}{b_{n,m,\gamma}} $$
  2. 杂波抑制： 应用改进的动目标显示 (MTI) 算法（IIR 高通滤波器）以抑制静态杂波。 $$ ( \tilde{\boldsymbol{F}}_{\mathrm{BS}} )_{n,m} = \frac{1}{a_0} \left( \sum_{i=0}^{I} b_i ( \grave{\boldsymbol{F}}_{\mathrm{BS}} )_{n,m-i} - \sum_{j=1}^{J} a_j ( \tilde{\boldsymbol{F}}_{\mathrm{BS}} )_{n,m-j} \right) $$
  3. 时延-多普勒处理： 计算周期图以估计目标距离和速度。 $$ \left(\mathrm{Per}_{\gamma}\right)_{k_{\tau},k_{f}} =\frac{1}{N M_s} \left| \sum_{m=0}^{M_s-1}\sum_{n=0}^{N-1} (\tilde{\boldsymbol{F}}_{\mathrm{BS},\gamma})_{n,m}\, w[n,m]\, e^{j2\pi \frac{n k_{\tau}}{N_{\mathrm{Per}}}} e^{-j2\pi \frac{m k_{f}}{M_{\mathrm{Per}}}} \right|^2 $$
  4. 微多普勒处理：

    在杂波抑制之后，微多普勒分析直接在每个距离单元的慢时间流上进行。首先，通过 IFFT 形成时延-时间矩阵：

    $$ \left(\boldsymbol{R}_{\mathrm{BS}}\right)_{k_{\tau},m} =\frac{1}{N}\sum_{n=0}^{N-1} \left(\tilde{\boldsymbol{F}}_{\mathrm{BS}}\right)_{n,m}\,e^{\,j2\pi \frac{n k_{\tau}}{N}} $$

    然后，选择一个工作距离单元 \(k_{\tau}^\star\) 并计算短时傅里叶变换 (STFT)：

    $$ \left(\boldsymbol{G}\right)_{m,k_f} =\sum_{\ell=0}^{M_w-1} r_{\mathrm{BS}}\!\left[mM_H+\ell\right]\; w_\mathrm{md}[\ell]\; e^{-j2\pi \frac{k_f\,\ell}{M_{\mathrm{md}}}} $$

    然后计算微多普勒谱：

    $$ \left( \mathrm{SPT} \right) _{m,k_f}=\frac{1}{M_w}\left| \left( \boldsymbol{G} \right) _{m,k_f} \right|^2 $$

UE 通信接收

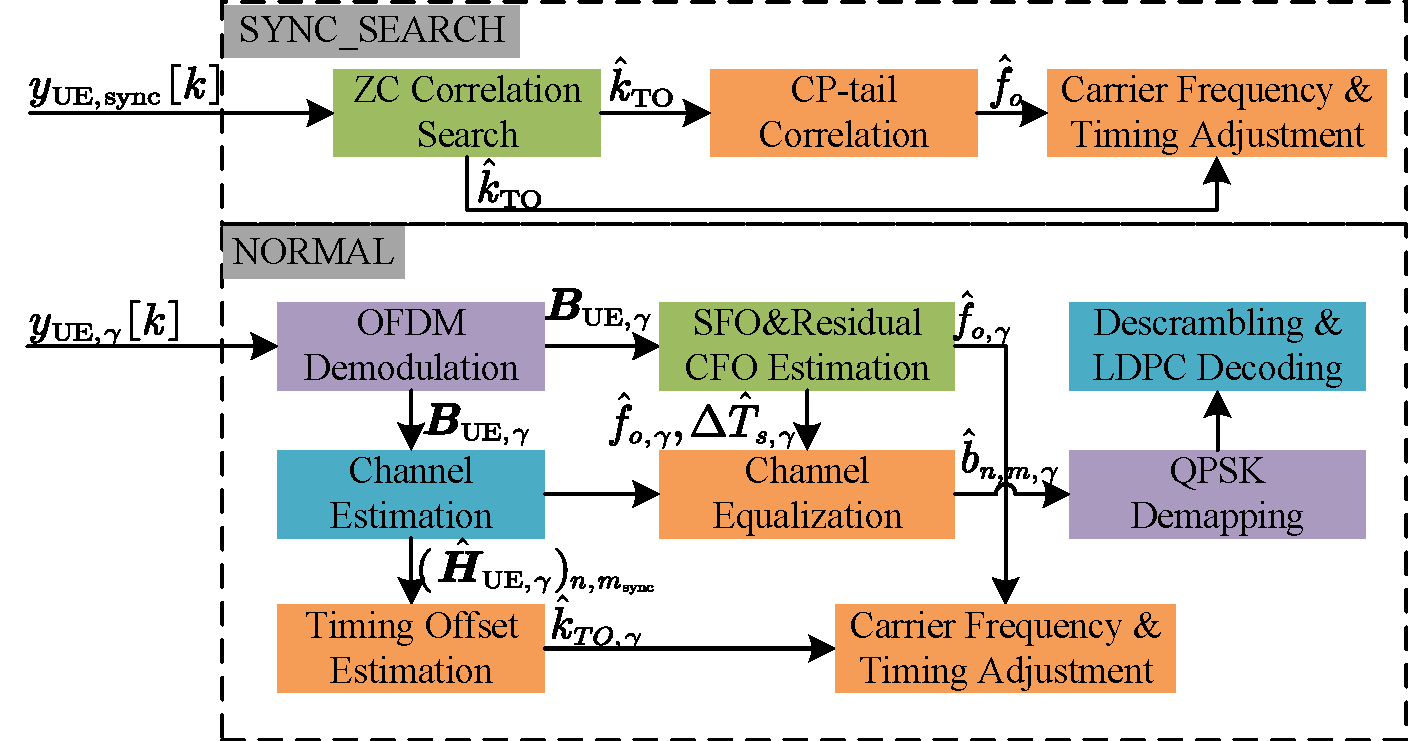
UE Processing Flow Graph

图 6. UE 通信接收框图。

UE 在两种状态下运行：

SYNC_SEARCH 状态

UE 以逐块方式运行。在每次迭代中，它获取一块样本并执行以下操作：

  1. 帧检测与定时估计： 与已知的 Zadoff–Chu (ZC) 同步符号 \(s_{\mathrm{ZC}}[k]\) 进行滑动相关： $$ r[k]=\sum_{i=0}^{N_s-1}{y_{\mathrm{UE},\mathrm{sync}}\left[ k+i \right] s_{\mathrm{ZC}}^{*}\left[ i \right]} $$ 归一化相关能量 \(r_N[k]\) 中的峰值指示帧边界和初始定时偏差 \(\hat{k}_{\mathrm{TO}}\)： $$ r_N[k]=\frac{|r[k]|^2}{\sum_{n=0}^{N_{\mathrm{corr}}}|r[k]|^2} $$
  2. 粗频偏估计： 利用跨越多个符号的 CP 尾部相关性来估计分数倍频偏 \(\hat{f}_o\)： $$ \hat{f}_o=\frac{\mathrm{arg}\!\bigl( r_{\mathrm{CP}} \bigr)}{2\pi T} $$
  3. 校正： 通过数字频率调节或 OCXO 调整以及样本对齐（填充/丢弃）来校正估计的偏差。

NORMAL 状态

一旦同步，UE 转换到 NORMAL 状态以处理帧：

  1. OFDM 解调： 移除 CP 并执行 FFT 以获得频域符号： $$ \left( \boldsymbol{B}_{\mathrm{UE},\gamma} \right)_{n,m} = b_{n,m,\gamma} \left( \boldsymbol{H}_{\mathrm{UE},\gamma} \right)_{n,m} + \left( \boldsymbol{Z}_{\mathrm{UE},\gamma} \right)_{n,m} $$
  2. 信道估计： 使用 ZC 符号估计信道响应： $$ (\hat{\boldsymbol{H}}_{\mathrm{UE},\gamma})_{n,m_{\mathrm{sync}}}=\frac{\left( \boldsymbol{B}_{\mathrm{UE},\gamma} \right) _{n,m_{\mathrm{sync}}}}{z_n} $$ 全帧信道估计通过对同步符号 \(m_{\mathrm{sync}}\) 处的估计插值获得： $$ (\hat{\boldsymbol{H}}_{\mathrm{UE},\gamma})_{n,m}=(\hat{\boldsymbol{H}}_{\mathrm{UE},\gamma})_{n,m_{\mathrm{sync}}}\exp \bigl( j2\pi ( m-m_{\mathrm{sync}} )( \hat{f}_{o,\gamma}T_O-n\Delta fN_s\Delta \hat{T}_{s,\gamma} ) \bigr) $$
  3. CFO/SFO 跟踪： 通过导频相位误差的加权线性回归 (WLS) 来跟踪残留载波频率偏差 (CFO) 和采样频率偏差 (SFO)： $$ \hat{\boldsymbol{\theta}}_\gamma = \big( \boldsymbol{A}_\gamma^{{T}} \boldsymbol{W}_\gamma \boldsymbol{A}_\gamma \big)^{-1} \boldsymbol{A}_\gamma^{{T}} \boldsymbol{W}_\gamma \boldsymbol{\varphi}_{{UE},\gamma} $$
  4. 均衡与解码： 通过单抽头频域均衡实现信道均衡： $$ \hat{b}_{n,m,\gamma}=\frac{\left( \boldsymbol{B}_{\mathrm{UE},\gamma} \right) _{n,m}}{(\hat{\boldsymbol{H}}_{\mathrm{UE},\gamma})_{n,m}} $$ 然后，计算 LLR，解扰并进行 LDPC 解码以恢复有效载荷。

UE 双站感知

双站感知的信号处理涉及重构未知的调制符号和执行空口 (OTA) 同步。

调制符号重构

重构的 QPSK 数据符号是通过对均衡后的符号 \(\hat{b}_{n,m,\gamma}\) 进行硬判决获得的：

$$ \tilde{b}_{n,m,\gamma} = \frac{1}{\sqrt{2}}\big( \operatorname{sgn}(\mathrm{Re}\{\hat{b}_{n,m,\gamma}\}) + j\operatorname{sgn}(\mathrm{Im}\{\hat{b}_{n,m,\gamma}\}) \big) $$

OTA 同步

双站感知需要通过无线链路实现鲁棒实时同步。OpenISAC 实现了低复杂度的空口 (OTA) 同步方案：

  1. 分数定时估计： 使用 Quinn 算法细化定时偏差，从时延域峰值获得分数估计 \(\hat{\delta}_{\tau}\)。总定时偏差估计为： $$ \hat{\tau}_{o,\gamma} = \frac{\hat{\delta}_{\tau}+k_{\max ,\gamma}}{f_s} $$
  2. SIO 跟踪： 通过对 \(\Gamma_W\) 帧窗口上的定时偏差执行线性回归来估计采样间隔偏差 (SIO) \(\epsilon_{\mathrm{SIO},w}\)： $$ \tilde{k}_{\tau,\gamma_w+\ell} \approx \epsilon_{\mathrm{SIO},w}\,\ell + \hat{k}_{\tau,\gamma_w} $$
  3. 递归更新： 维护累积感知定时偏差 \(\hat{k}^{\mathrm{sens}}_{\tau,\gamma}\) 的平滑估计以避免抖动： $$ \hat{k}^{\mathrm{sens}}_{\tau,\gamma} = \hat{k}^{\mathrm{sens}}_{\tau,\gamma-1} + \hat{\epsilon}_{\mathrm{SIO},w-1} - \hat{k}_{\mathrm{TO},\gamma-1} + \mu_\gamma e_\gamma $$ 其中 \(\mu_\gamma e_\gamma\) 是基于跟踪误差的反馈校正项。
  4. 信道补偿： 将估计的定时偏差和 SIO 应用于双站信道矩阵以补偿同步误差： $$ \left( \tilde{\boldsymbol{F}}_{\mathrm{UE},\gamma} \right) _{n,m} = \left( \boldsymbol{F}_{\mathrm{UE},\gamma} \right) _{n,m} e^{j2\pi n\Delta f\left( \hat{k}_{\tau ,\gamma}^{\mathrm{sens}}+mN_s\Delta \hat{T}_{as,w-1} \right)} $$